题解 P4115 Qtree4

发表于 | 更新于 | 分类于 | 阅读次数：

题面

Qtree4

题意:
$n$个点，每个点有一个颜色，黑或白
每次查询最大白点间距离
带修改
$n=10^5,q=2*10^5$

(相信大家边分治，LCT等 $O(nlog^2n)$做法都会了)

但是这里有一个常数巨大的$O(nlogn)$做法

前置芝士

1.全局平衡二叉树(详见2007年论文Qtree问题解法的一些研究)

在一些静态树上查询，修改问题中，LCT能做到超大常数的$O(logn)$,而树链剖分只能做到$O(log^2n)$，原因何在?

因为LCT整棵树可以看做一个大的spaly$splay$，仍然可以进行势能分析
而树剖只能做到单条链最优(局部最优)，但是全局并没有最优

全局平衡二叉树 就完成了把LCT强行静态的过程

轻重链剖分的部分是一样的，但是我们对每一条链建立一颗二叉搜索树
给每一个点一个权值为轻儿子$size$之和$+1$(自己)，然后每次找重心递归建树

证明每个点的深度为$O(logn)$很简单，每次调到父亲子树大小(包括虚子树)至少翻倍

然后就可以开开心心的以一个$log$的做法做树剖题了

2.把任意一棵树转化为树上距离不变的二叉树

相信大家都学过边分治吧，那我就不讲了

直接上图

原树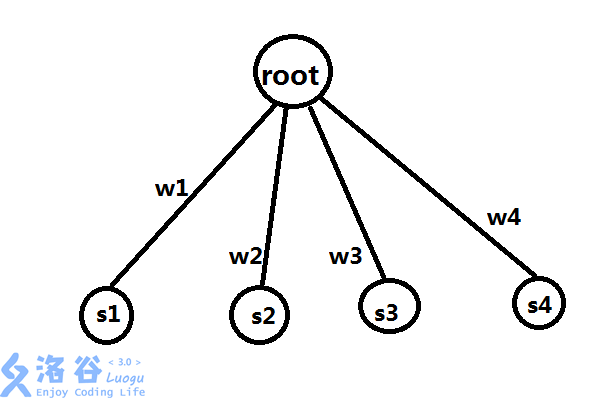

二叉树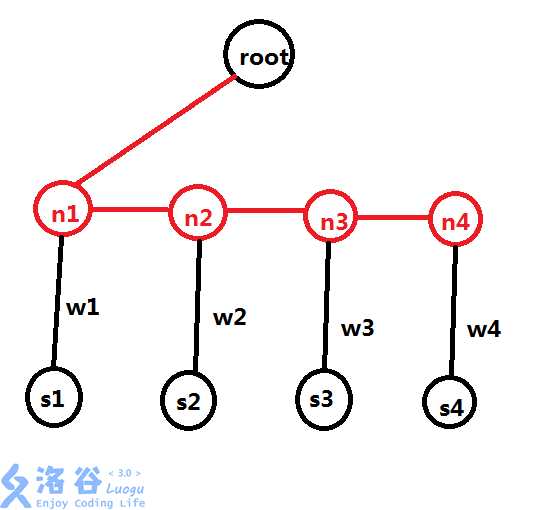

其中红点为新建的虚点，红边的边权均为0
对于每一个点，它的儿子都这样处理，然后就变成有$2n$个点的二叉树了
感受一下，是不是很神奇?

正题开始

首先考虑最强的树上分治链分治
对于每一条链维护$lca$在这条链上的最大白点距离
直接做的做法:

以下为了方便，点$x$的轻子树和表示以$x$为根的子树去掉它的重子树，点$x$的轻子树表示以它的一个轻儿子为根的子树，$dfn$表示$dfs$序

对于每一个点$x$维护一个堆，记录$x$的每个轻子树内任意黑点到$x$的距离的最大值，

线段树维护答案
对于$dfn$区间$[l,r]$,记录三个值:
1.$lmax$:所有$dfn$为$[l,r]$点的轻子树和内的所有黑点到$dfn$为$l$的点的距离最大值
2.$rmax$:同理，表示所有$dfn$为$[l,r]$点的轻子树和内的所有黑点到$dfn$为$l$的点的距离最大值
3.$ans$:表示所有$dfn[lca]\in [l,r]$ 的黑点的距离最大值

区间合并:线段树上$x$的左儿子为$ls$，右儿子为$rs$

边界:点$x$对应区间$[L,L]$ $D_1=$堆内的最大值，$D_2=$堆内的次大值(来自两个不同轻子树)(若没有为$-\infty$)

若$x$为白点

(自己到自己，自己到最远的，最远的到次远的)
否则

然后我们发现其实距离堆内维护的就是每个轻儿子线段树顶的$lmax+dist(x,son)$

每条链的答案可以记在另一个堆里，询问时直接查即可

复杂度分析:

dist(i,j):发现总是在求祖先-后代距离，所以深度减一下$O(1)$
建树O(n)
每次修改$O(logn)$条链，每次线段树$O(logn)$,修改距离堆$O(logn)$，修改记答案的堆$O(logn)$总复杂度$O(nlog^2n)$
每次查询$O(1)$获取堆顶即可
总复杂度$O(qlog^2n+n)$

愚蠢的$log^2$做法到此结束

考虑降为一个$log$

首先直接上全局平衡二叉树可以把线段树部分降为单次询问$O(logn)$
答案堆直接不要了，全局平衡二叉树的$ans$带上轻子树和内的答案即可

然后是距离堆
我们发现距离堆内的点的个数为轻儿子个数
所以把它转成二叉树就不用堆来维护了

惊不惊喜，意不意外

然后就可以一个$log$愉快的过掉了

其实bb了这么一大堆，代码十分好写

码风丑，大佬轻喷

另外有一个细节，我的二叉查找树结合了线段树的特点，(有点像宗法树)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int inf = 1000000000;
char buf[1 << 20];
char *S = buf, *T = buf;
inline char gc() {
    if(S == T) T = buf + fread(buf, 1, 1 << 20, stdin), S = buf;
    return S == T ? EOF : *S ++;
}
inline int read() {
    int f = 1, c;
    unsigned a = 0;
    for(c = gc(); c != '-' && (c < '0' || c > '9'); c = gc());
    if(c == '-') c = gc(), f = -1;
    for(; c <= '9' && c >= '0'; c = gc()) a = (a << 1) + (a << 3) + (c ^ '0');
    return f == 1 ? a : (~a) + 1;
} // 快速读入
int size[200010], wson[200010], lson[200010], lsize[200010], dep[200010];
struct node {
    int ls, rs, ans, L, R, lmax, rmax, fa;
} t[400010]; //二叉查找树结构体
int nowcnt;
int st[200010], cnt;//记录当前链
int n, m;
vector<pair<int, int> > son[100010];//记录原树
inline void addedge(int u, int v) {
    if(wson[u] == 0) wson[u] = v;
    else lson[u] = v;
}
inline void dfs(int now, int f) {//建立新树
    addedge(now + n, now);
    for(int i = 0; i < son[now].size(); i++)
        if(son[now][i].first == f) {
            son[now].erase(son[now].begin() + i);
            break;
        }
    for(int i = 0; i < son[now].size(); i++) dep[son[now][i].first + n] = dep[now], dep[son[now][i].first] = dep[now] + son[now][i].second, dfs(son[now][i].first, now);//其实此时dep已经可以求出
    for(int i = 1; i < son[now].size(); i++) addedge(son[now][i - 1].first + n, son[now][i].first + n);
    if(son[now].size()) addedge(now, son[now][0].first + n);
}
inline void dfs1(int now) {//树剖的第一次dfs
    size[now] = 1;
    if(wson[now]) dfs1(wson[now]), size[now] += size[wson[now]];
    if(lson[now]) dfs1(lson[now]), size[now] += size[lson[now]];
    if(size[lson[now]] > size[wson[now]]) swap(lson[now], wson[now]);
    lsize[now] = size[lson[now]] + 1; 
}
inline int build(int l, int r) {//对st[l...r]建立二叉树
    if(l == r) return t[st[l]].L = t[st[l]].R = st[l]; //此处有压行(逃)
    int sum = 0, cnt = 0, ans;
    for(int i = l; i <= r; i++) sum += lsize[st[i]];
    sum >>= 1;
    for(int i = l; i <= r; i++) {
        cnt += lsize[st[i]];
        if(cnt >= sum) {//找到重心
            if(i == l) i++;//要是不加，哼哼
            ans = ++nowcnt;
            t[ans].ls = build(l, i - 1);
            t[ans].rs = build(i, r);
            t[t[ans].ls].fa = t[t[ans].rs].fa = ans;
            t[ans].L = st[l], t[ans].R = st[r];
            return ans;
        }
    }
}
int root;
inline void dfs2(int now) {
//st[1...cnt]保存当前链，st[0]为链头的父亲(为0则链头为根)
    st[++cnt] = now;
    if(wson[now]) dfs2(wson[now]);
    else {
        int rt = build(1, cnt);
        if(st[0] == 0) root = rt;
        else t[rt].fa = st[0], t[st[0]].ls = t[st[0]].rs = rt;
        cnt = 0;
    }
    st[0] = now;
    if(lson[now]) dfs2(lson[now]);
}
int col[200010];
inline void up(int x) {
    node &now = t[x];
    if(now.L == now.R) {//叶子节点
        int D = t[now.ls].lmax + dep[lson[x]] - dep[x];//因为是二叉树，所以不会有D2
        now.ans = t[now.ls].ans;
        if(col[x]) now.ans = max(now.ans, now.lmax = now.rmax = max(D, 0));
        else now.lmax = now.rmax = D;
    }
    else {//非叶子节点
        now.lmax = max(t[now.ls].lmax, t[now.rs].lmax + dep[t[now.rs].L] - dep[now.L]);
        now.rmax = max(t[now.rs].rmax, t[now.ls].rmax + dep[now.R] - dep[t[now.ls].R]);
        now.ans = max(max(t[now.ls].ans, t[now.rs].ans), t[now.ls].rmax + t[now.rs].lmax + dep[t[now.rs].L] - dep[t[now.ls].R]);
    }
}
inline void init(int now) {
    if(t[now].L == t[now].R) {
        if(t[now].ls) init(t[now].ls);
    }
    else init(t[now].ls), init(t[now].rs);
    up(now);
}
int main() {
    // freopen("hehezhou.in", "r", stdin);
    // freopen("hehezhou.out", "w", stdout);
    t[0].lmax = t[0].ans = t[0].rmax = -inf;
    n = read();
    for(int i = 1, u, v, w; i < n; i++) u = read(), v = read(), w = read(), son[u].push_back(make_pair(v, w)), son[v].push_back(make_pair(u, w));
    dfs(1, 0);
    nowcnt = n << 1;
    dfs1(n + 1);
    dfs2(n + 1);
    // for(int i = 1; i <= n << 1; i++) printf("%d %d\n", wson[i], lson[i]);
    for(int i = 1; i <= n; i++) col[i] = 1;
    // for(int i = 1; i <= nowcnt; i++) printf("%d : ls = % d, rs = %d, fa = %d, L = %d, R = %d\n", i, t[i].ls, t[i].rs, t[i].fa, t[i].L, t[i].R);
    init(root);
    nowcnt = n;//在这之前表示二叉搜索树节点当前使用量，之后表示白点个数
    m = read();
    for(int i = 1; i <= m; i++) {
        char opt;
        for(opt = gc(); opt != 'C' && opt != 'A'; opt = gc());
        if(opt == 'A') nowcnt ? printf("%d\n", t[root].ans) : puts("They have disappeared.");
        else {
            int v;
            v = read();
            if((col[v] ^= 1) == 0) nowcnt--;//压行大法好
            else nowcnt++;
            for(; v; v = t[v].fa) up(v);
        }
    }
    return 0;//完结撒花
}

最后祝大家$rp$++