题面
不得不说,浙江神队选拔赛真是年年毒瘤
首先你需要有一点导数的知识,否则可能看不懂
第一问很简单,建个图跑个最大流就好了(如果这都不会还敢来肝zjoi???)
第二问
有一个很$fAKe$的想法:
因为费用不是一次函数,而是二次函数,并且我们观察到$a,b>=0$
所以我先想到的是把每个酿酒点的费用强行离散,就是分成一个个区间,然后源点向每个酿酒点连很多条边,再跑费用流
因为导函数单调不降,所以理论上是可以做到一定精度的然而我们观察到毒瘤出题人要求输出分数让误差降为0???
显然分的越细误差越小
考虑分的份数无限趋于0
此时费用即为导数
然后就可以开个集合维护当前单位费用最小的酿酒点
然后二分出当单位费用涨到多少时,集合内点会变化(要么是有新点加入,要么是有一个点跑满流)
然后更新集合并进行下一轮操作然而二分还是只能做到一定精度(貌似乘上一个奥妙重重的系数可以二分整数,但我不知道是不是对的,而且复杂度好像是假的)正解!
观察一下解法2,就会发现当集合内点不变时,产酒量(当前流量)和费用呈线性关系,并且当集合内点变化时,费用的一次函数会发生变化
所以搞一个函数$y = f(x)$表示单位费用(导数)不超过x时,最大流是多少
那么$f(x)$可以被分成若干段,每段均为一次函数(最多$2n$段)
然后可以用类似积分的方式搞出最小费用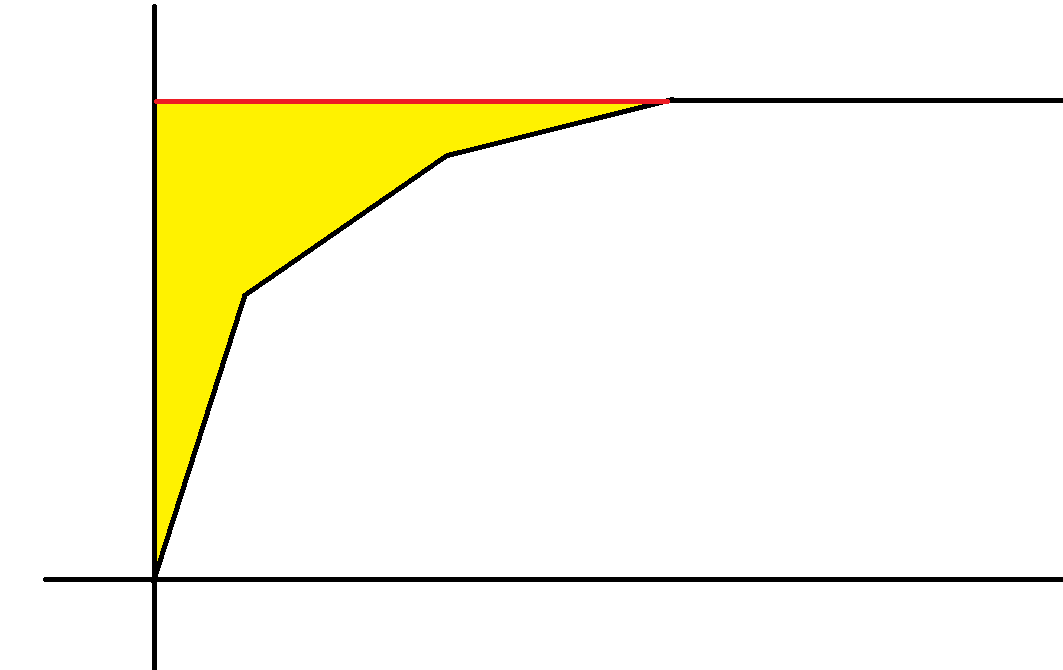
考虑怎么搞出这个函数
如果只有二次函数的费用,那么f(x)会形成一个类似上凸壳的图像
然后考虑分治,每次求出最左一次函数和最右一次函数的交点,如果再图像上则该点是区间内唯一断点,否则递归处理两个子区间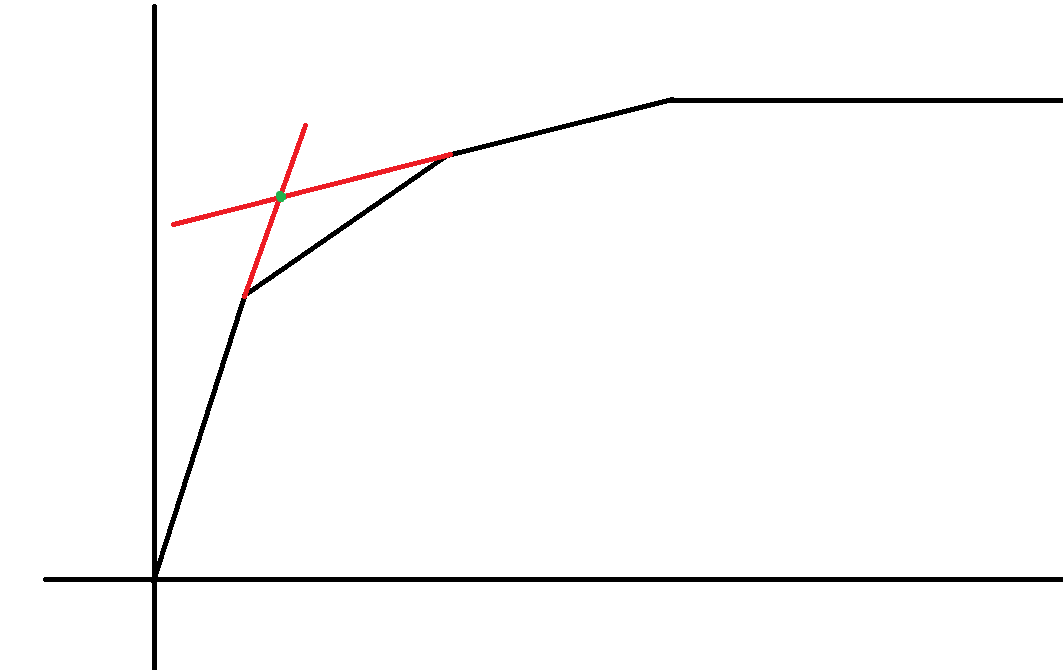
然后考虑一次函数
发现b只会是0, 1, 2, 3(详细数据范围见bzoj)
只要强行设1, 2, 3为断点即可
记得加上左右边界的f(x)之差(见代码)
复杂度$O(n\times$网络流$)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
using namespace std;
typedef long long ll;
typedef double db;
const db feps = 1e-11, eps = 1e-9;
inline ll gcd(ll a, ll b) {
return a == 0 || b == 0 ? a | b : gcd(b, a % b);
}
struct frac {
ll a, b; //仔细看题发现要开ll
inline frac(ll _a = 0, ll _b = 1) {
int g = gcd(_a, _b);
a = _a / g, b = _b / g;
}
friend inline frac operator + (frac a, frac b) {
return frac(a.a * b.b + a.b * b.a, a.b * b.b);
}
friend inline frac operator - (frac a, frac b) {
return frac(a.a * b.b - a.b * b.a, a.b * b.b);
}
friend inline frac operator * (frac a, frac b) {
return frac(a.a * b.a, a.b * b.b);
}
friend inline frac operator / (frac a, frac b) {
return frac(a.a * b.b, a.b * b.a);
}
inline operator db () {
return 1.0l * a / b;
}
};
int dis[210], s, t;
int a[110], b[110], c[110], d[110], ed[110][110];
struct edge {
db f;
int v, nxt;
} e[3010];
int tot, head[210], cur[210];
int n, m;
inline void addedge(int u, int v, db c) {
e[++tot] = edge{c, v, head[u]};
head[u] = tot;
e[++tot] = edge{0, u, head[v]};
head[v] = tot;
}
inline int bfs() {
queue<int> q;
memset(dis, -1, sizeof dis);
dis[s] = 0;
q.push(s);
memcpy(cur, head, sizeof head);
while(!q.empty()) {
int now = q.front();
q.pop();
for(int i = head[now]; i; i = e[i].nxt) {
if(~dis[e[i].v] || e[i].f < feps) continue;
dis[e[i].v] = dis[now] + 1;
q.push(e[i].v);
}
}
return dis[t] != -1;
}
inline db dfs(int now, db limit) {
if(now == t) return limit;
db ans = 0;
for(int &i = cur[now]; i; i = e[i].nxt) {
if(e[i].f < feps || dis[e[i].v] != dis[now] + 1) continue;
db lala = dfs(e[i].v, min(limit, e[i].f));
limit -= lala, ans += lala;
e[i].f -= lala, e[i ^ 1].f += lala;
if(limit < feps) return ans;
}
return ans;
}
inline pair<frac, frac> dinic(db lambda) {
tot = 1;
memset(head, 0, sizeof head);
for(int i = 1; i <= n; i++) {
if(a[i] == 0) {
if(b[i] < lambda) addedge(s, i, c[i]);
}
else {
db w = (lambda - b[i]) / 2 / a[i];
if(w > feps) addedge(s, i, min(1.0 * c[i], w));
}
}
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) if(ed[i][j]) addedge(i, j + n, 1e9);
for(int i = 1; i <= m; i++) addedge(i + n, t, d[i]);
while(bfs()) dfs(s, 1e9);
frac K, B;
for(int i = 1; i <= n; i++) {
if(dis[i] == -1) {
if(a[i] == 0) {
if(b[i] < lambda) B = B + frac(c[i]);
}
else {
if(b[i] > lambda) B = B + frac();
else if(a[i] * 2 * c[i] + b[i] > lambda)
K = K + frac(1, a[i] * 2), B = B - frac(b[i], a[i] * 2);
else B = B + frac(c[i]);
}
}
}
for(int i = 1; i <= m; i++) if(dis[i + n] != -1) B = B + frac(d[i]);
return make_pair(K, B);
} //dinic板子
vector<pair<frac, frac> > v;
inline void solve(pair<frac, frac> fl, pair<frac, frac> fr) { //分治找断点
if(fl.first == fr.first && fl.second == fr.second) return;
frac px = (fl.second - fr.second) / (fr.first - fl.first);
pair<frac, frac> fml = dinic((db)px - eps), fmr = dinic((db)px + eps);
if(fmr.first == fr.first && fmr.second == fr.second) {
v.push_back(make_pair(px, fml.second + fml.first * px));
} else {
solve(fl, fml);
solve(fmr, fr);
}
}
int main() {
scanf("%d%d", &n, &m);
s = 0, t = n + m + 1;
for(int i = 1; i <= n; i++) scanf("%d%d%d", a + i, b + i, c + i);
for(int i = 1; i <= m; i++) scanf("%d", d + i);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) scanf("%d", &ed[i][j]);
frac ans, sum;
cout << (sum = dinic(1e9).second).a;//第一问
v.push_back(make_pair(frac(), 0));
for(int i = 1; i <= 3; i++) {
auto l = dinic(i - 1 + eps), r = dinic(i - eps);
solve(l, r);
v.push_back(make_pair(frac(i), r.second + frac(i) * r.first));
}
solve(dinic(3 + eps), dinic(1e9));//找断点
for(int i = 1; i < v.size(); i++) {
auto l = dinic((db)v[i].first - eps), r = dinic((db)v[i].first + eps), _l = dinic((db)v[i - 1].first + eps);//std=c++11(滑稽
ans = ans + v[i].first * ((r.first - l.first) * v[i].first + r.second - l.second);
ans = ans + (v[i].second - v[i - 1].first * _l.first - _l.second) * frac(1, 2) * (v[i].first + v[i - 1].first);//积分
}
if(ans.a < 0) ans.a = -ans.a, ans.b = -ans.b;
return cout << ans.a << '/' << ans.b << endl, 0;
}